Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124


በዚህ ጦማር ላይ የምንጠቀምባቸው ያንዳንድ ቃሎች ትርጉሞች የሚገኙት ማትጎኖች (polygons) በሚለው ጦማር ውስጥ ስለሆነ፣ ይህን ጦማር ከማንበብወ በፊት ማትጎኖች (polygons) የሚለውን ጦማር ቢያንስ ቢያንስ በገረፍታ ይመልከቱት።
ስሌጎን (triangle) ማለት ሶስት ጎኖች (three sides) እንዲሁም ሶስት ዘዌወች (three angles) ያሉት ማትጎን (polygon) ማለት ነው። ከዚህም ስሌጎናዊ (triangular) የሚለውን ቃል እናገኛለን። ለምሳሌ ያህል ስሌጎናዊ ቅርጽ (triangular shape) ማለት የስሌጎን ቅርጽ ያለው ማለት ነው።

የማናችውም ስሌጎን ሶስቱም ዘዌወች ጠቅላላ ድምር ሁልጊዜም 180 ጉለም (180 degrees) ነው።


ሁሉም ዘዌወቹ እኩል የሆኑ (ማለትም ሦስቱም ዘዌወቹ እያንዳንዳቸው 60o የሆኑ) ስሌጎን፣ እኩልዘዌያም ስሌጎን (equiangular triangle) ይባላል። በእኩል ዘዌያም ስሌጎን ላይ ሦስቱም ጎኖች ርዝመታቸው እቅጩን እኩል ነው። በዚህም ምክኒያት እኩልዘዌያም ስሌጎን ሌላኛው ስሙ እኩልጎናም ስሌጎን (equilateral triangle) ነው።

ሁለቱ ዘዌወቹ እኩል (two equal angles) ስለዚህም ሁለቱ ጎኖቹ እኩል (two equal sides) የሆኑ ስሌጎን እኩል እግራም ስሌጎን (isosceles triangle) ይባላል።

እኩልእግራም ስሌጎን (isosceles triangle) ማለት ቢያንስ ሁሉቱ ጎኖቹ እኩል የሆኑ ስሌጎን ማለት ነው። እኩልጎናም ስሌጎን (equilateral triangle) ደግሞ ሶስቱም ጎኖቹ እኩል ናቸው። ስለዚህም እኩልጎናም ስሌጎን ሦስቱም ጎኖቹ እኩል የሆኑ እኩልእግራም ስሌጎን ነው ማለት ነው። በሌላ አባባል እኩልጎናም ስሌጎን (equilateral triangle) ልዩ እኩልእግራም ስሌጎን (special isosceles triangle) ነው ማለት ነው። አሁንም በሌላ አባባል እኩልእግራም ስሌጎን ሲባል እኩልጎናም ስሌጎንንም ያጠቃላል ወይም ይጨምራል ማለት ነው።

ሮጋ (ማለትም ማዕዘን) ከሚለው የኦሮምኛ ቃል ሩንጋ (perpendicular) የሚለውን ቃል እናገኛለን። ለምሳሌ ያህል ሩንጋ ዘዌ (right angle) ማለት እሴቱ እቅጩን 90o የሆነ ዘዌ ማለት ሲሆን፣ ሩንጋ መስመሮች (perpendicular lines) ደግሞ 90o የሚሠሩ መስመሮች ማለት ነው።
አንደኛው ዘዌው ሩንጋ ዘዌ (right angle) የሆነ፣ ማለትም እሴቱ እቅጩን 90o የሆነ ስሌጎን ሩንጋ ዘዌ ስሌጎን (right angle triangle) ወይም ባጭሩ ሩንጋ ስሌጎን (right triangle) ይባላል። በሩንጋ ስሌጎን ላይ ለሩንጋ ዘዌው ተቃራኒ (opposite) የሆነው ጎን ቲባ (hypotenuse) ሲባል፣ የቀሩት ሁለቱ ጎንኖች ደግሞ እግሮች (legs) ይባላሉ። ቲባ (hypotenuse) የሚለው ቃል የተገኘው ተባ (ማለትም ያጋደለ) ከሚለው የኦሮምኛ ቃል ነው።

መጠኑ በ 0o እና 90o መካከል የሆነ ዘዌ ሹል ዘዌ (acute angle) ይባላል። መጠኑ በ 90o እና 180o መካከል የሆነ ዘዌ ደግሞ ዝርጥጥ ዘዌ (obtuse angle) ይባላል።

ሁለቱ ዘዌወቹ ሹል ዘዌወች (acute angle) የሆኑ (ማለትም ከ 90o ያነሱ) ስሌጎን ሹል ስሌጎን (acute triangle) ይባላል። አንዱ ዘዌው ዝርጥጥ ዘዌ (obtuse angle) የሆነ (ማለትም ከ 90o የበለጠ) ስሌጎን ደግሞ ዝርጥጥ ስሌጎን (obtuse triangle) ይባላል።

ማናቸውም ዘዌወቹ እኩል ያልሆኑ እንዲሁም ማናቸውም ጎኖቹ እኩል ያልሆኑ ስሌጎን እኩልቢስ ስሌጎን (scalene triangle) ይባላል። እኩልቢስ ስሌጎን ሹል (acute)፣ ሩንጋ (right) ወይም ዝርጥጥ (obtuse) ሊሆን ይችላል።




ተመሳሳይ (similar) ማለት የሚመሳሰሉ ማለት ነው። ተመሳሳይ የሚለውን ቃል አካሄድ በመከተል ደግሞ ተካካይ (congruent) የሚለውን ቃል እናገኛለን። ተካካይ ማለት በቀርጽም በመጠነም እኩል የሆነ፣ ልክክ ብሎ የሚገጥም ማለት ነው። ተካካይ (congruent) እና ታካኪ (tangent) እንዳይምታቱብወት።
similar = ተመሳሳይ
similar triangles = ተመሳሳይ ስሌጎኖች
similar polygons = ተመሳሳይ ማትጎኖች
congruent = ተካካይ
congruent triangles = ተካካይ ስሌጎኖች
congruent polygons =ተካካይ ማትጎኖች
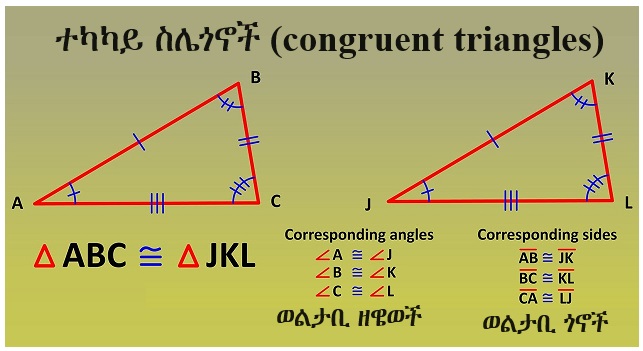
ተካካይ ስሌጎኖች (congruent triangles) ማለት በቅርጽም በመጠንም እኩል የሆኑ፣ ማለትም ርስበራሳቸው በትክክል ልክክ የሚሉ ስሌጎኖች ማለት ነው። በሌላ አባባል ተካካይ ስሌጎኖች (equal congruent triangles) ማለት ወልታቢ ዘዌወቻችው እኩል የሆኑ (equal corresponding angles) እንዲሁም ወልታቢ ጎኖቻቸው እኩል የሆኑ (equal corresponding sides) ስሌጎኖች ማለት ነው። ወልታቢ (corresponding) ማለት በተመሳሳይ ቦታ ላይ የሚገኝ ማለት ሲሆን፣ ቃሉ የተገኘው ደግሞ ወል (የጋራ) እና ከተበ (ጻፈ) ከሚሉት ነው።
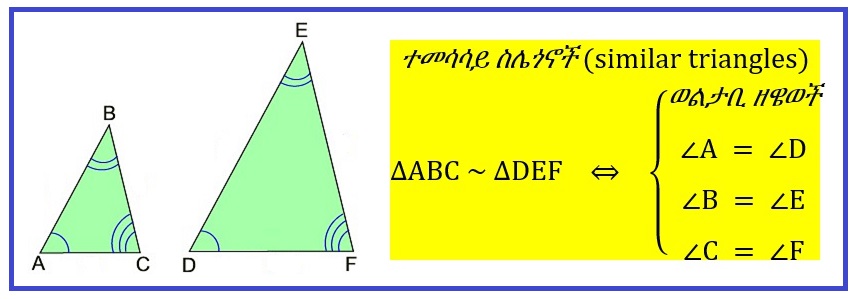
በሌላ አባባል በኩል ደግሞ ተመሳሳይ ስሌጎኖች (similar triangles) ማለት በቅርጽ ተመሳሳይ የሆኑ፣ በመጠን ግን አኩል ሊሆኑም፣ ላይሆኑም የሚችሉ ስሌጎኖች ማለት ነው። በሌላ አባባል ተመሳሳይ ስሌጎኖች (similar triangles) ማለት ወልታቢ ዘዌወቻቸው እኩል የሆኑ (equal corresponding angles) ወልታቢ ጎኖቻቸው ግን እኩል ሊሆኑም ላይሆኑም የሚችሉ ስሌጎኖች ማለት ነው።
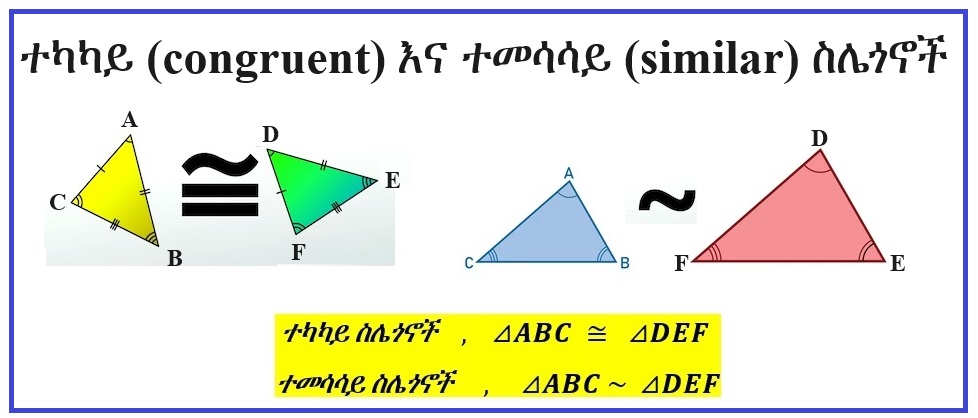
ሁለት ስሌጎኖች ተካካይ (congruent) ይሆኑ ዘንድ ወልታቢ ዘዌወቻቸው እኩል፣ እንዲሁም ወልታቢ ጎኖቻቸው እኩል መሆን አለባቸው። እነዚህ ሁለት ስሌጎኖች ተመሳሳይ (similar) ይሆኑ ዘንድ ግን የሚጠበቅባቸው ወልታቢ ዘዌወቻቸ ብቻ እኩል እንዲሆኑ ነው። ስለዚህም ተካካይ የሆኑ ሁሉ ተመሳሳይ ናቸው፣ ተመሳሳይ የሆኑ ሁሉ ግን ተካካይ አይደሉም ማለት ነው። በሌላ አባባል ተካካይ ስሌጎኖች (congruent triangles) ወልታቢ ጎኖቻቸው እኩል የሆኑ ልዩ ተመሳሳይ ስሌጎኖች (special similar triangles) ናቸው ማለት ነው።
ተመሳሳይ ስሌጎኖች (similar triangles) ተመሳሰሉ እንደምንል፣ ተካካይ ስሌጎኖች (congruent triangles) ደግሞ ተካከሉ እንላለን። የተካካይነት ምልክት ሲሆን፣ የተመሳሳይነት ምልክት ደግሞ
ነው።
እኩልእግራም ስሌጎን (isosceles triangle) በሚለው ክፍል ላይ እንደተመለከትነው፣ ሲማክ (base) ማለት መሠረት እንደ ማለት ሲሆን፣ ቃሉ የተገኘው ደግሞ ሰመከ (ማለትም ተጠጋ፣ ተደገፈ፣ ጥግ ያዘ፣ ድጋፍ ያዘ) ከሚለው የግእዝ ቃል ነው።
የስሌጎን ሲማክ (base of triangle) ማለት በታች በኩል የሚገኘው የስሌጎኑ ጎን (side) ማለት ነው። በስሌጎን ሲማከ (base) እና ከሲማኩ በተቃራኒ በሚገኘው የስሌጎኑ ፊጣ (vertex) መካከል ያለው ሩንጋ ርርቀት (perpendicular distance) ደግሞ የስሌጎኑ ሩንጋ ከፍታ (perpendicular height) ወይም ባጭሩ ክፍታ (height) ይባላል።
base = ሲማክ
height = ከፍታ
perpendicular height = ሩንጋከፍታ

ስሌጎንን ባማዟዟር ማናቸንም የስሌጎኑን ጎን ሲማክ (base) ማድረግ ይቻላል።

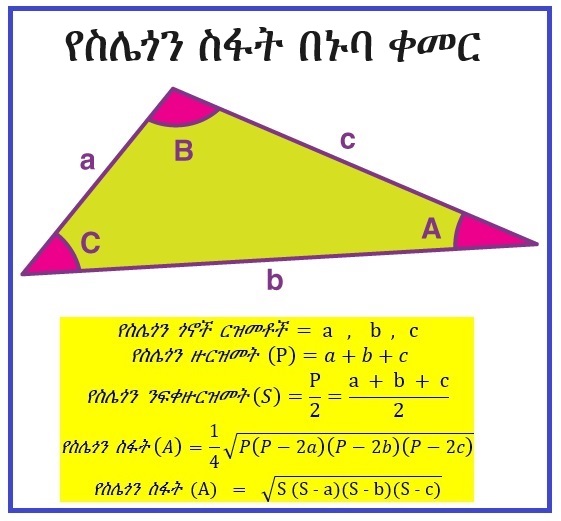
የማናችውም ስሌጎን ስፋት (area of triangle) በስሌጎኑ ሲማክ (base of triangle) እና ከፍታ (height of triangle) አንጻር በሚከተለው ቀመር (formula) ይሰጣል።


የስሌጎን ሁሉም ጎኖች ርዝመቶች ድምር የስሌጎኑ ዙርዝመት (perimeter) ሲባል፣ የስሌጎኑ ዝርዝመት ግማሽ (እኩሌታ) ደግሞ ንፍቀዙርዝመት (semi-perimeter) ይባላል። የማናችውም ስሌጎን ስፋት (area) በስሌጎኑ ዙርዝመት (perimeter) እና በስሌጎኑ ንፍቀዙርዝመት (semi-perimeter) አንጻር በሚከተለው ቀመር (formula) ይሰጣል።

የስሌጎንን ስፋት በስሌጎኑ ዙርዝመት (perimeter) እና ንፍቀዙርዝመት (semi-perimeter) አንጻር የሚሰጠው ቀመር በነጮች አጠራር የሄሮን ቀመር (Heron’s formula) ይባላል። ይህም ቀመር የተሰየመው ባንደኛው ወይም በሁለተኛው መቶመን (century) እስክንድርያ (Alexandria) ውስጥ ይኖር በነበረው ሄሮን ዘእስክንድርያ (Heron of Alexandria) ስም ነው። መቶመን (century) የሚለው ቃል የተገኘው መቶ እና ዘመን ከሚሉት ነው፣ አስርመን (decade)፣ ሺመን (millennium) እንዲሉ።
የሄሮንን ቀመር (Heron’s formula) የቀመረው ግሪካዊው ሒሳብሲነኛ (mathematician) ሄሮን ዘአስክንድርያ (Heron of Alexandria) ነው ቢባልም፣ እውነታው ግን እስክንድር መቄዶናዊ (Alexander the great) ኑባን (Nubia) ከመያዙ በፊት ሺ ዓመታት አስቀድመው የስሌጎን ቅርጽ (triangle shape) ያላቸውን ግዙፍ ኑቢሳወችን (pyramids) የገነቡት ኑባውያን (Nubians) ቀመሩን ለብዙ ሺ ዓመታት ይጠቀሙበት የነበሩ መሆኑ ነው። ኑቢሳ (pyramid) የሚለው ቃል የተገኘው ኑብያ እና ኩይሳ ከሚሉት ቃሎች ነው።
የግሪክ ፍልስፍና (Greek philosophy) የሚባለው አንድም ሳይቀር ሁሉም እስክንድር መቄዶናዊን ተከትለው የገቡ ግሪኮች የሰረቁት ፍልስፍና መሆኑን “የተሰረቀ ቅርስ፡የግሪክ ፍልስፍና የተሰረቀ የኑባ ፍልስፍና ነው” (Stolen Legacy: Greek philosophy is stolen Egyptian Philosophy) የሚለውን በጊወርጊስ ያቆብ (George James) የተጻፈውን መጽሐፍ ያንብቡ። እኔም መስፍን አረጋ ይህን ድንቅ መጽሐፍ ወደ አማረኛ መልሸዋለሁ፣ አልታተመም እንጅ።
ስለዚህም ሄሮን (Heron)፣ አሪስጣጣሊስ (Aristotle)፣ በጥሌሞስ (Ptolemy) እና የመሳሰሉት ጥንታዊ ግሪኮች የሰውን ሥራ የራሳቸው አስመስለው የሚያቀርቡ፣ ዐይናቸውን በጨው ያጠቡ፣ የለየላቸው መንታፊወች (plagiarists) ስለነበሩ፣በነዚህ መንታፊወች ስም የሚጠሩ ሥራወችን ሁሉ አፍሪቃውያን መጥራት ያለባቸው በኑብያውያን ስም ነው። በዚህም ምክኒያት በምንተፋ ወደር የሌላቸው ነጮች የሄሮን ቀመር (Heron’s formula) የሚሉትን እኔ መስፍን አረጋ የኑባ ቀመር (Nubian formula) ብየዋለሁ።

ገንገና (theory) ማለት በንግሊዘኛ ቲወሪ የሚባለው ሲሆን ቃሉ የተገኘው ገነገነ (ፈራ፣ ታዘበ፣ ጠረጠረ፣ መረመረ) ከሚለው ያማረኛ ቃል ነው። ግሱም ሲረባ ገነገነ (theorize)፣ ግንጉን (theorized)፣ ገንጋኝ (theorizer, theorist)፣ ግንግነት (theorizing) እያለ ይሄዳል።
እንዲሁም ግንገና (theory) ከሚለው ገንጊሳ (theorem) የሚለውን ቃል እናገኛለን። ገንጊሳ ማለት በሒሳብ የተረጋገጠ (ማለትም አሁንም፣ ወደፊትም፣ ሁሌም ርግጠኛ የሆነ) ሒሳባዊ ግንገና ማለት ነው።
theory – ግንገና
theorem – ገንጊሳ
ሩንጋ ስሌጎን (right triangle) በተሰኘው ክፍል ላይ እንደተመለከትነው፣ አንደኛው ዘዌው ሩንጋ ዘዌ (right angle) የሆነ፣ ማለትም እሴቱ እቅጩን 90o የሆነ ስሌጎን ሩንጋ ዘዌ ስሌጎን (right angle triangle) ወይም ባጭሩ ሩንጋ ስሌጎን (right triangle) ይባላል።
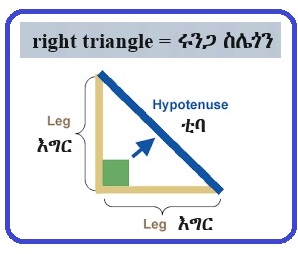
በሩንጋ ስሌጎን ላይ ለሩንጋ ዘው ተቃራኒ (opposite) የሆነው ጎን ቲባ (hypotenuse) ሲባል፣ የቀሩት ሁለቱ ጎንኖች ደግሞ እግሮች (legs) ይባላሉ። ቲባ (hypotenuse) የሚለው ቃል የተገኘው ተባ (ማለትም ያጋደለ) ከሚለው የኦሮምኛ ቃል ነው።
ሩንጋ ስሌጎንን (right triangle) በተመለከተ የስሌጎኑን እግሮች (legs) ርዝመቶች ከስሌጎኑ ቲባ (hypotenuse) ርዝመት ጋር የሚያዛምድ ገንጊሳ (theorem) አለ። ይህም ገንጊሳ በፈርንጆቹ አጠራር ፓይታጎራስ ገንጊሳ (Pythagoras theorem, Pythagorean theorem) ይባላል።
ፓይታጎራስ (Pythagoras) ኖረ የሚባለው ባምስተኛው ዓመተ ዓለም ነው። ኑባወች (Nubians) ደግሞ ታላላቁቹን ኑቢሳወች (pyramids) የገነቡት ፒታጎራስ ኖረ ከሚባልበት ዘመን በፊት ቢያንስ፣ ቢያንስ ሁለት ሺ ዓመታት አስቀድመው ነው። ኑባወች ደግሞ የሩንጋ ስሌጎንን ሦስቱንም ጎኖች የሚያዘምደውን መሠረታዊ ገንጊሳ ሳያውቁ፣ ኑቢሳወቹን ሊገነቡ በጭራሽ አይችሉም። ስለዚህም ፓይታጎራስም ልክ እንደ ሌሎቹ የጥንታዊ ግሪክ “ፈላስፋ”ተብየወች የሰውን ሥራ የራሱ አስመስሎ ያቀረበ መንታፊ (plagiarist) ባይሆን እንጅ ቢሆን አያስደንቅም። በመሆኑም፣ ይህን ገንጊሳ እኔ መስፍን አረጋ የኑባ ገንጊሳ (Nubian theorem) ወይም ካልቶና ገንጊሳ (square theorem) ብየዋለሁ።

ካልቶና ገንጊሳን (square theorem, Pythagorean theorem) የሚያሟሉ ማናቸውም ሦስት ቁጥሮች ካልቶና ስሌቻን (square triplets, Pythagorean triplets) ይባላሉ። ለምሳሌ ያህል ቁጥሮች 3፣ 4 እና 5 ካልቶና ስሌቻን (square triplets) ናቸው።
ስሌቻን (triplet) የሚለው ቃል የተገኘው ሠለስቱ (ሦስቱ) ከሚለው የግእዝ ቃል ነው፣ ክሌቻን (doublet)፣ ስሌቻን (triplet)፣ ራቤቻን (quadruplet)፣ ሃሜቻን (quintuplet)፣ ሳዴቻን (sextuplet)፣ ሳቤቻን (septuplet)፣ ሳሜቻን (octuplet)፣ ታሴቻን (nonuplet)፣ አሴቻን (decuplet) እንዲሉ። ለተጨማሪ ማብራሪያ የቁጥሮች ስያሜወች የሚለውን ጦማር ይመልከቱ።

መስፍን አረጋ
mesfinamharic.com
mesfin.arega@gmail.com