ክብና ፉንባ (Circle & Ellipse)

ማሳሰቢያ

በዚህ ጦማር ላይ የምንጠቀምባቸው ያንዳንድ ቃሎች ትርጉሞች የሚገኙት ማትጎኖች (polygons)፣ ስሌጎኖች (triangles) እና ራቤጎኖች (quadrilaterals) በሚሉት ጦማሮች ውስጥ ስለሆነ፣ ይህን ጦማር ከማንበብወ በፊት እነዚህን ጦማሮች ቢያንስ ቢያንስ በገረፍታ ይመልከቱ።

ማግዘም እና ሚንሰም 

ማግዘም (maximum) ማለት የመጨረሻ ትልቅ ማለት ሲሆን፣ ቃሉ የተገኘው ግዙፍ ከሚለው በመነሳትና የንግሊዘኛውን ቃል አካሄድ በመከተል ነው።  እንዲሁም ሚንሰም (minimum) ማለት የመጨረሻ ትንሽ ማለት ሲሆን፣ ቃሉ የተገኘው እንስ (ያነሰ) ከሚለው ቃል በመነሳትና የንግሊዘኛውን ቃል አካሄድ በመከተል ነው። የማግዘም ግስ ሲረባ መገዘመ (maximize)፣ ምግዝም (maximized)፣ መግዛሚ (maximizer)፣ ምግዘማ (maximization) እያለ ሲሄድ፣ የሚንሰም ግስ ሲረባ ደግሞ መነሰመ (minimize)፣ ምንስም (minimized)፣ መንሳሚ (minimizer)፣ ምንሰማ (minimization) እያለ ይሄዳል።

maximum  = ማግዝም
maximize = መገዘመ
minimum =ሚንሰም
minimize  = መነሰመ

ሱርፊክ እና ኢዶ 

ሱራ (ስዕል) እንዲሁም ፈኪ (ስዕል) ከሚሉት የኦሮምኛ ቃሎች ሱርፊክ (figure) የሚለውን ቃል እናገኛለን።  ሱርፊክ ማለት ንድፍ፣ ስዕል ማለት ሲሆን፣ ግሱም ሲረባ ሶረፈከ (to figure)፣ ሱርፍክ (figured)፣ ሶርፋኪ (figuring)፣ ሱርፈካ(figuring)፣ ሱርፍከት (figuring)፣ ሱርፋኬ፣ ሱርፋኮሽ እያለ ይሄዳል። ሱርፊክሳ (figurehead) ማለት ደግሞ የይስሙላ መሪ ማለት ነው።    

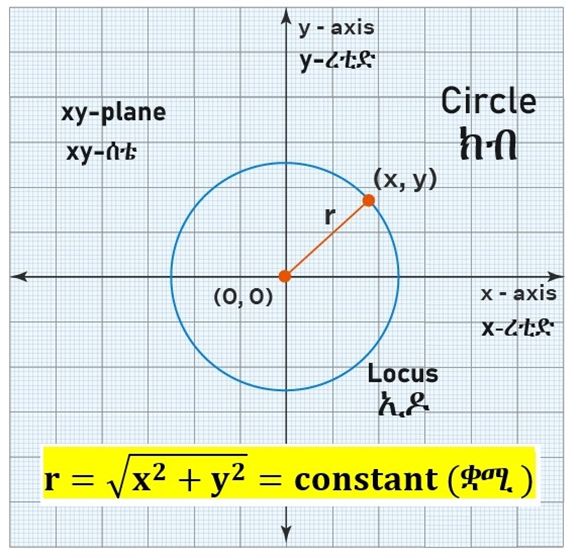
ኢዶ ማለትም ቦታ የሚለው የኦሮምኛ ቃል locus የሚለውን የንግሊዘኛ ቃል ይተካልናል።  ኢዶ (locus) ማለት የተወሰኑ መስፈርቶችን ወይም እኩልታወችን (equations) የሚያሟሉ ነጥቦች ባንድነት የሚሠሩት ክብን (circle) ወይም ሉልን (sphere) የመሰለ ቂሳሲናዊ ሱርፊክ (geometrical figure) ማለት ነው። 

figure = ሱርፊክ
locus = ኢዶ
locus of points = የነጥቦች ኢዶ

ሰቴ እና አልሰቴ

በግእዝ ሰቲት ማለት ለጥ ያለ፣ ቀጥ ያለ፣ የተዘረጋ ማለት ነው፣ ሰተቶ፣ ሰቲት ሑመራ እንዲሉ።  ስለዚህም ሰቲት፣ ሰታይ፣ሰቴ የሚሉት ቃሎች የእንግሊዘኛውን plane ይተኩልናል። ሰቴ ያልሆነ ደግሞ አልሰቴ (non-plane) ይባላል።  እንዲሁም ሰቴ (plane) ከሚለው ቃል ወልሰቴ (coplanar) እና አልወልሰቴ (noncoplanar) የሚሉትን ቃሎች እናገኛለን።  ወልሰቴ ማለት አንድ ሰቴ የሚጋሩ፣ የወል የሆነ ሰቴ ያላቸው ማለት ነው፣ ውልሰቴ ነጥቦች (coplanar points) እንዲሉ። አልወልሰቴ ማለት ደግሞ በተለያዩ ሰቴወች ላይ የሚውሉ፣ አንድ ሰቴ የማይጋሩ ማለት ነው፣ አልወልሰቴ ነጥቦች (noncoplanar points) እንዲሉ።  

plane  = ሰቴ
non-plane = አልሰቴ
coplanar points =ወልሰቴ ነጥቦች
noncoplanar points = አልወልሰቴ ነጥቦች

መስመር እና ዐጽቅ 

ቀጠ ያለ ከሚለው ቀጤ (straight) የሚለውን እናገኛለን።  ከዚህም ቀጤ መስመር(straight line) የሚለውን እናገኛለን። ቀጤ መስመር ማለት ቀጥ ያለ መስመር ማለት ነው። ቀጤ መስመር አብዛኛውን ጊዜ ባጭሩ መስመር ይባላል። 

የተወሰነ ርዝመት ያለው የመስመር ክፍል ዐጽቅ (segment) ይባላል። ከዚህም የቀጤ መስምር ዐጽቅ (straight line segment)፣ የኩርባ መስመር ዐጽቅ (curved line segment) የሚሉትን እናገኛለን።    የቀጤ መስመር ዐጽቅ አብዛኛውን ጊዜ ባጭሩ ቀጣጽቅ ወይም ዐጽቅ ይባላል።

segment = ዐጽቅ
straight line segment =የቀጤ መስመር ዐጽቅ
curved line segment = የኩርባ መስመር ዐጽቅ

የክብ ብያኔ

ክብ ማለት ሁሉም ነጥቦቹ ከመሃሉ (center) እኩል ርቀት ላይ የሚገኙ ሰቲታዊ ሱርፊክ (planar figure) ነው።  በኢዶ (locus) ቋንቋ ደግሞ ክብ ማለት መሃል (center) ከሚባል አንድ ነጥብ ያላቸው ርቀት እኩል የሆነ የወልሰቴ ነጥቦች ኢዶ (locus of coplanar points) ነው ተብሎ ይበየናል (defined)።

ዐብይ ደጋን እና ንዑስ ደጋን

እንደ መስመር (line) ሲታይ ክብ ልዩ የሆነ ኩርባ መስመር (curve line) ነው።  የዚህ ኩርባ መስመር ዐጽቅ (segment) [ማለትም የተወሰነ ርዝመት ያለው ክፍል] ደግሞ ደጋን (arc) ይባላል።  በሌላ አባባል ደጋን (arc) ማለት የተወሰነ ርዝመት ያለው የክብ መስመር ዐጽቅ (segment of a circle) ማለት ነው።

ርዝመቱ እቅጩን (precisely) የክብን ግማሽ የሆነ የክብ ዐጽቅ ንፍቀክብ (semicircle) ይባላል። ርዝመቱ የክብን ግማሽ የሚበልጥ ደጋን ዐብይ ደጋን (major arc) ይባላል። ርዝመቱ ከክብ ግማሽ የሚያንስ ደጋን ደግሞ ንዑስ ደጋን (minor arc) ይባላል። 

ዊታር፣ ታክመር እና ቆርመር

ሁለቱ ጫፎቹ በክብ ጠርዝ ላይ የሚወሉ ማናቸውም የቀጤ መስመር ዐጽቅ (straight line segment) የክቡ ዊታር (chord) ይባላል።  በሌላ አባባል የክብ ዊታር (chord) ማለት በክብ ላይ የሚገኙ ማናችወንም ሁለት ነጥቦች በቀጥታ የሚያገናኝ የቀጤ መስመር ዐጽቅ ማለት ነው።   ዊታር (chord) የሚለው ቃል የተገኘው ወተረ (ገተረ፣ ወጠረ) ከሚለው የግእዝ ቃል ነው።  በግእዝ አውታር ማለት የተወጠሩ፣ የተገተሩ ማለት ነው፣ የበገና አውታር እንዲሉ።   

ክብን ሁለት ነጥቦች ላይ ቆርጦ የሚያልፍ ቀጤ መስመር(straight line) ቆርመር (secant, secant line) ሲባል፣ ክብን አንደ ነጥብ ላይ ብቻ የሚነካ ቀጤ መስመር (straight line) ደግሞ ታክመር (tangent, tangent line) ይባላል። ቆርመር የሚለው ቃል የተገኘው “ቆራጭ መስመር” ከሚለው ሐረግ ሲሆን፣ ታክመር የሚለው ቃል የተገኘው ደግሞ “ታካኪ መስመር” ከሚለው ሐረግ ነው። 

የክብ ቆርመር (secant) ከቡን የሚቆርጥባቸው ነጥቦች ቁርመራ ነጥቦች (points of secancy) ሲባሉ፣ የክብ ታክመር (tangent) ክቡን የሚታከክበት ነጥብ ደግሞ ትክመራ ነጥብ (point of tangency) ይባላል።

አክዘንግ እና ገማዘንግ

አክባቢ ዘንግ ከሚለው ሐረግ አክዘንግ (radius) የሚለውን ቃል ስናገኝ፣ ገማሽ ዘንግ ከሚለው ሐረግ ደግሞ ገማዘንግ (diameter) የሚለውን ቃል እናገኛለን። አክዘንግ ማለት ከክብ እምብርት ወይም ማዕከል (center) እስከ ክብ ጠርዝ የሚሰመር፣ ማለትም ከማዕከሉ ተነስቶ ክብን የሚያካብብ መስመር ማለት ነው።  ገማዘንግ ማለት ደግሞ በክብ ማዕከል ላይ በማለፍ ክብን ለሁለት እኩሌታ የሚገምስ መስመር ማለት ነው።  የገማዘንግ ርዝመት የአክዘንግን ርዝመት ሁለት እጥፍ ነው።

ቶካድ ክብ

ቶካድ (unit) ማለት ሜትር (meter)፣ ግራም (gram) እና ደቂቃን የመሳሰለ የመጠን መግለጫ ማለት ሲሆን፣ ቃሉ የተገኘው ቶኮ (ማለትም አንድ) ከሚለው የኦሮምኛ ቃል እና አንድ ከሚለው ያማረኛ ቃል ነው። 

አክዘንጉ (radius) 1 መሀሉ (center) ደግሞ (0,0) ላይ የሆነ ክብ ቶካድ ክብ (unit circle) ይባላል።  ወደፊት በሌላ ጦማር ላይ እንደምንመለከተው ቶካድ ክብ የሚያገለግለው ስሌግሲናዊ ቀዘዶችን (trigonometric functions) ከካርቴዛዊ ቀንጆች (Cartesian coordinates) ጋር ለማዛመድ ነው። 

የማትጎን ዙርዝመት እና የክብ ሠቅርመት

የማትጎን ሁሉም ጎኖች (sides) ጠቅላላ ርዝመት፣ ማለትም ማትጎኑ ዙርያውን ያለው ጠቅላላ ርዝመት ዙርዝመት (perimeter) ይባላል።  ዙርዝመት የሚለው ቃል የተገኘው ዙር እና ርዝመት (አርዝመት) ከሚሉት ቃሎች ነው።

በሌላ በኩል ደግሞ አንድ ክብ ዙርያውን ያለው ጠቅላላ ርዝመት ሠቅርመት (circumference) ይባላል።  ሠቅርመት የሚለው ቃል የተገኘው ሠቅ (ቀበቶ) ከሚለው የግእዝ ቃል እና ርዝመት ከሚለው ቃል ነው።  ስለዚህም የክብ ሠቅርመት (circumference) ማለት የክቡ ዙርዝመት (perimeter) ማለት ነው።  በዚህም ምክኒያት ሠቅርመት አንዳንድ ጊዜ ዙርዝመት ይባላል። 

የክብ ሠቅርመት በክቡ አክዘንግ (radius) እሴት (value) ላይ የሚመይፍ (depend) ማለትም የሚመካ ሲሆን፣ በሚከተለው ቀመር ይሰጣል። መየፈ (depend) የሚለው ቃል የተገኘው ታፈየ (ታመነ) ከሚለው የግእዝ ቃል ሲሆን፣ ገሱም ሲረባ መየፈ (depend)፣ ምይፍ (ምዩፍ) [depended, dependent]፣ መያፊ፣ ምየፋ (depending)፣ ምይፈት (dependency)፣ ምያፌ፣ ምያፎሽ እያለ ይሄዳል።

መሃልጌ ዘዌ እና ወጣቢ ደጋን

ፊጣው (vertex) በክብ መሃል (center) ላይ የሆነ ዘዌ መሃልጌ ዘዌ (central angle) ይባላል።  መሃልጌ የሚለው ቃል የተገኘው መሃል ከሚለው እና ጌ (ቦታ) ከሚለው የግእዝ ቃል ነው፣ ራስጌ፣ ግርጌ እንዲሉ።

በመሃልጌ ዘዌ (central angle) ጎኖች (sides) የሚታቀፍ የክብ ደጋን መሃልጌ ዘዌውን ወጥቦታል (subtend) ይባላል።  ወጠበ (subtend) የሚለው ቃል የተገኘው ወጠረ እና ከበበ ከሚሉት ሲሆን፣ ግሱም ሲረባ ወጠበ (subtend)፣ ውጥብ (ውጡብ) [subtended]፣ ወጣቢ፣ ውጠባ (subtending)፣ ውጥበት፣ ውጣቤ፣ ውጣቦሽ እያለ ይሄዳል። 

የሚወጠበው መሃልጌ ዘዌ (central angle) እሴት ከ 180^o ያነሰ ወጣቢ ደጋን (subtending arc) ንዑስ ደጋን (minor arc) ሲሆን፣ የሚወጠበው መሃልጌ ዘዌ (central angle) እሴት ከ 180^o  የበለጠ ወጣቢ ደጋን (subtending arc) ደግሞ ዐብይ ደጋን (major arc) ነው።  የሚወጠበው መሃልጌ ዘዌ (central angle) እሴት እቅጩን 180^o የሆነ ወጣቢ ደጋን (subtending angle) ደግሞ ንፍቀክብ (semicircle) ነው። 

የደጋን ርዝመት

የደጋን ርዝመት (arc length) ደጋኑ በሚወጥበው (subtend) መሃልጌ ዘዌ (central angle) እሴት (value) እና በክቡ ሠቅርመት (circumference) ላይ የሚመይፍ (depend) ማለትም የሚመካ ሲሆን፣ በሚከተለው ቀመር ይሰጣል። የቀመሩም መልክ (form) የደጋኑ መሃልጌ ዘዌ (central angle) እሴት የተሰጠው በጉለም (degree) ወይም በጃራ (radian) እንደመሆኑ ይለያያል።

የክብ ስፋት

የክብ ስፋት በክቡ አክዘንግ (radius) እሴት (value) ላይ የሚመይፍ (depend) ማለትም የሚመካ ሲሆን፣ በሚከተለው ቀመር ይሰጣል።

የክብ ኩርማን

በሁለት አክዘንጎች (radii) እና አክዘንጎቹን በሚያገናኛቸው ደጋን (arc) የታቀፈ (enclosed) የክብ ክፍል ኩርማን (sector) ይባላል።  ባማረኛ ኩርማን ማለት አንድ አራተኛ ክፍል እንደ ማለት ነው፣ ኩርማን እንጀራ እንዲሉ። 

የክብ ኩርማን ስፋት 

የክብ ኩርማን (sector) ስፋት በክቡ አክዘንግ (radius) እና የኩርማኑ ደጋን (arc) በሚውጥበው (subtend) መሃልጌ ዘዌ (central angle) ላይ የሚመይፍ (depend) ማለትም የሚመካ ሲሆን፣ በሚከተለው ቀመር ይሰጣል። የቀመሩም መልክ (form) የመሃልጌ ዘዌ (central angle) እሴት የተሰጠው በጉለም (degree) ወይም በጃራ (radian) እንደመሆኑ ይለያያል።

የክብ ዐጽቅ

በዊታር (chord) እና ዊታሩን በሚወጥበው (subtend) ደጋን (arc) የታቀፈ (enclosed) የክብ ክፍል የክብ ዐጽቅ (segment of a circle) ወይም ባጭሩ ዐጽቅ (segment) ይባላል። 

ገማዘንግ (diameter) ያልሆነ ማናቸውም የክብ ዊታር (chord)፣ ክቡን ለሁለት ዐጽቆች ይከፍለዋል።  እነዚህም የክቡ ዐጽቆች ዐብይ ዐጽቅ (major segment) እና ንዑስ ዐጽቅ (minor segment) ይባላሉ። 

በሌላ በኩል ደግሞ የክብ ገማዘንግ (diameter) ክቡን እቅጩን (precisely) እኩል ለሆኑ ሁለት ዐጽቆች ይከፍለዋል።  እነዚህም የክቡ ዐጽቆች ንፍቀክቦች (semicircles) ይባላሉ።  

የክብ ዐጽቅ ስፋት

የክብ ዐጽቅ (segment) ስፋት በክቡ አክዘንግ (radius) እና የዐጽቁ ደጋን (arc) በሚውጥበው (subtend) መሃልጌ ዘዌ (central angle) ላይ የሚመይፍ (depend) ማለትም የሚመካ ሲሆን፣ በሚከተለው ቀመር ይሰጣል። የቀመሩም መልክ (form) የመሃልጌ ዘዌ (central angle) እሴት የተሰጠው በጉለም (degree) ወይም በጃራ (radian) እንደመሆኑ ይለያያል።

የዐጽቅ ስፋት (segment area) ቀመር (formula) እንዴት እንደተገኘ ከሚከትለው ሱርፊክ (figure) መረዳት ይቻላል።

ሩማል እና ጢያ

ሂሩ (መከፋፈል) ከሚለው የኦሮምኛ ቃል ሂራ (mid, middle) የሚለውን መሀከልነትን የሚያመለክት ፊልጡፍ (prefix) እናገኛለን።  ሂራ ማለት መሃል እንደማለት ነው።  ለምሳሌ ያህል የዐጽቅ ሂራነጥብ (midpoint) ማለት በዐጽቁ መሃል (middle) ላይ የሚገኝ ነጥብ ማለት ነው። በዐጽቅ ሂራነጥብ (midpoint) ላይ በማለፍ ዐጽቁን ለሁለት እኩል ክፍሎች የሚከፍል መስመር ደግሞ የዐጽቁ ክሌገማሽ(bisector) ይባላል።

ሮጋ (ማለትም ማዕዘን) ከሚለው የኦሮምኛ ቃል ሩንጋ (perpendicular) የሚለውን ቃል እናገኛለን። ለምሳሌ ያህል ሩንጋ መስመሮች (perpendicular lines) ማለት ሩንጋዘዌ (right angle) ማለትም  90^o የሚሠሩ መስመሮች ማለት ነው።  

ርርቀት ማለት መራራቅ እንደማለት ነው።  ለምሳሌ ቦታ ሀ ለቦታ ለ ሩቅ ነው እንደምንል፣ በቦታ ሀ እና በቦታ ለ መካከል ያለው ርርቀት (ማለትም መራራቅ) ከፍተኛ ነው እንላለን።     

በክብ መሃል (center) እና በክቡ ዊታር ሂራነጥብ (midpoint of chord) መካክል ያለው ሩንጋዊ ርርቀት(perpendicular distance) ሩማል (apothem) ይባላል። ሩማል የሚለው ቃል የተገኘው ሩንጋ (perpendicular) እና መሃል (center)  ከሚሉት ቃሎች ነው።  

በዊታር ሂራነጥብ (midpoint of chord) እና ዊታሩን በሚወጥበው (subtend) ደጋን ሂራነጥብ (midpoint of arc) መካክል ያለው ሩንጋዊ ርርቀት (perpendicular distance) ደግሞ ጢያ (sagitta) ይባላል።  ጢያ ማለት በኦሮምኛ ቀስት ማለት ነው።    

የደጋን ጢያ (sagitta) የደጋኑን ጥልቀት (depth) ማለትም ጐድጓዳነት መለኪያ ነው። 

የማናቸውም ደጋን (arc) ጢያ (sagitta) ርዝመት ደጋኑ በሚወጥበው (subtend) መሃልጌ ዘዌ (central angle) እና በደጋኑ ክብ አክዘንግ (radius) አንጻር በሚከተለው ቀመር (formula) ይሰጣል። 

ወልመሃል ክቦች

መሃላቸው (center) ያው (same) የሆነ፣ ማለትም አንድ መሃል ያላቸው ወልሰቴ ክቦች (coplanar circles) ማለትም በያው (same) ሰቴ (plane) ላይ የሚውሉ ክቦች ወልመሃል ክቦች (concentric circles) ይባላሉ።  በሌላ አባባል ወልመሃል ክቦች ማለት መሃላቸውም አንድ፣ ሰቴያቸውም አንድ የሆነ ክቦች ማለት ነው።    

ውስጥክትብ እና ውጭክትብ

ከተበ (ማለትም ጻፈ) የሚለው ቃል scribe የሚለውን የንግሊዘኛ ቃል ይተካልናል።  ግሱም ሲረባ ከተበ (scribe) ክትብ (ክቱብ) [scribed] ከታቢ (scribing)፣ ከተባ(scription) እያለ ይሄዳል።   

ውስጥ እና ከተበ (scribe) ከሚሉት ውስጥክትብ (inscribed) የሚለውን ቃል ስናገኝ፣  ውጭ እና ከተበ (scribe) ከሚሉት ደግሞ ውጭክትብ (circumscribed) የሚለውን ቃል እናገኛለን።

scribe  = ከተበ
inscribed = ውስጥክትብ
circumscribed =ውጭክትብ

ዳርጌ ዘዌ (ውስጥክትብ ዘዌ)

ፊጣው (vertex) ከክብ ዳር (edge) ላይ የሆነ፣ ጎኖቹ (sides) ደግሞ የክቡ ዊታሮች (chords) የሆኑ ዘዌ፣ ዳርጌ ዘዌ (inscribed angle) ይባላል። የዳርጌ ዘዌ ሌላኛው ስሙ ውስጥክትብ ዘዌ (inscribe angle) ነው። 

ውስጥክትብ እና ውጭክትብ ማትጎኖች

በክብ ውስጥ ተስሎ ፊጣወቹ (vertices) በክቡ ሠቅርመት (circumference) ላይ የሚውሉ ማትጎን (polygon) ውስጥክትብ ማትጎን (inscribed polygon) ይባላል።  በሌላ በኩል ደግሞ በክብ ውጭ ተስሎ ጎኖቹ (sides) የክቡ ታክምሮች (tangents) የሆኑ ማትጎን (polygon) ውጭክትብ ማትጎን (circumscribed polygon) ይባላል።  

ውስጥክትብ ማትጎንን (inscribed polygon) የሚከበው ክብ (circle) ውጭክትብክብ (circumscribed circle) ሲባለል፣ በውጭክትብ ማትጎን (circumscribed polygon) የሚከበብ ክብ (circle) ደግሞ ውስጥክትብክብ (inscribed circle) ይባላል። 

ማናችውንም የዘፈቀደ ማትጎን (arbitrary polygon) ውስጥመከተብ (inscribe) ወይም ውጭመከተብ (circumscribe) አይቻልም። 

በርግጥም አብዛኞቹ ማትጎኖች ውስጥም ሆነ ውጭ ሊከተቡ አይችሉም።  አንዳንድ ጊዜ ደግሞ ውስጥተከታቢ (inscribable) ማትጎን ውጭተከታቢ (circumscribable) ላይሆን ይችላል፣ እንዲሁም ውጭተከታቢ (circumscribable) ማትጎን  ውስጥተከታቢ (inscribable) ላይሆን ይችላል። 

በሌላ በኩል ግን ማናቸውንም የዘፈቀደ ስሌጎን (arbitrary triangle) ውስጥመከተብ (inscribe) እንዲሁም ውጭመከተብ (circumscribe) ይቻላል።

ማናቸውንም ደንብገኛ ማትጎን (regular polygon) ውስጥመከተብ (inscribe) እንዲሁም ውጭመከተብ (circumscribe) ይቻላል።

ፉንባ

ፉፉልያ ማለትም እንቁላል ከሚለው የወላይትኛ ቃል፣ እንዲሁም ቡጴ ማለትም እንቁላል ከሚለው የኦሮምኛ ቃል ፉንባ (ellipse) የሚለውን ቃል እናገኛለን። ፉንባ ማለት ሞላላ ክብ እንደ ማለት ነው።  የዱባ ቅርጽም እንደ ፉንባ ነው።

የፉንባ (ellipse) ግስ ፎነበ፣ ፉንብ፣ ፎናቢ፣ ፉነባ፣ ፉንበት፣ ፉናቤ፣ ፉናቦሽ እያለ ይሄዳል።  ፎነበ ማለት ፉንባ ሆነ ወይም ተደረገ ማለት ሲሆን፣ የንግሊዘኛ አቻ የለውም።  ክብ (circle) ይከበባል፣ ፉንባ (ellipse) ይፎነባል። 

ፉንባ (ellipse) ከሚለው ቃል ፉንባዊ (elliptic, elliptical)፣ ፉንባፊካ (ellipsoid)፣ ፉንባለኪ (ellipsometer)፣ ፉንባ ምሕዋር (elliptic orbit)፣ ፉንባ ምሳግ (elliptic integral)፣ ፉንባ ውልትመት (elliptic polarization) የመሳሰሉት ቃሎች እናገኛለን። 

የፉንባ ፉነባ

ማናቸውንም ፉንባ (ellipse) የሚከተለውን ደተራ (procedure) በመከተል በቀላሉ መፎነብ ይቻላል።  ደተራ (procedure) ማለት ቅደም ተከተል ማለት ሲሆን፣ ቃሉ የተገኘው ደረጃ እና ተራ ከሚሉት ነው።  ግሱም ሲረባ ደተረ፣ ድትር (ድቱር)፣ ደታሪ፣ ድተራ እያለ ሲሄድ፣ የንግሊዘኛ አቻ የለውም።  ደተረ ማለት ደተራ አዘጋጀ፣ ቅደም ተከተል አወጣ ማለት ነው።  

1. የተወሰነ ርዝመት ያለው ቀጭን ክር ማግኘትና ሁለቱ ጫፎቹ ላይ ቋጥሮወችን መሥራት ።
2. በሁለቱ ቋጠሮወች ውስጥ ሁለት ቀጭን ሚስማሮች፣ እስፒሎች (pins) ወይም እሾሆች ማስገባትና፣ ክሩን በማይገትር ሁኔታ እሾሆቹን ሌጣ ወረቀት ላይ እንዳይነቃነቁ አድርጎ መትከል።
3. በመጨረሻም ክሩን በእርሳስ ገትሮ በመያዝ ክሩ እንደተገተረ እርሳሱን ወረቀቱ ላይ ተጭኖ በእሾሆቹ ዙርያ ማዞር።

1. ሁለቱ እሾሆች የተተከሉባቸው ነጥቦች የፉንባው አቲኮች (foci) ይባላሉ።  አቲክ (focus) የሚለው ቃል የተገኘው አተከ ማለትም ሰበሰበ ከሚለው ያማረኛ ቃል ሲሆን፣ ግሱም ሲረባ አተከ፣ እትክ፣ አታኪ፣ እተካ እያለ ይሄዳል። 
2. በሁለቱ የፉንባው አቲኮች (foci) ላይ በማለፍ እስከ ፉንባው ዳርቻወች የሚሰመር የቀጤ መስመር ዐጽቅ (line segment) የፉንባው ዐብይ ረቲድ (major axis) ይባላል።  የዐብይ ረቲድ ግማሽ (ማለትም እኩሌታ) ደግሞ ንፍቀዐብይ ረቲድ ወይም ንፍቃብይ ረቲድ (semi-major axis) ይባላል።  ረቲድ (axis) የሚለው ቃል የተገኘው ተራዳ (የድንኳን ምሰሶ) ከሚለው ያማረኛ ቃል ሲሆን፣ ግሱም ሲረባ ረተደ፣ ርትድ (ርቱድ)፣ ረታዲ (ረታጅ)፣ ርተዳ እያለ ይሄዳል።      
3. የዐብይ ረቲድ (major axis) ሩንጋ ክሌገማሽ (perpendicular bisector) የሆነ፣ ማለትም ካብይ ረቲድ ጋር 90^o ዘዌ በመሰራት ዐብይ ረቲድን እኩሌታ የሚከፍል፣ ጫፉቹ ደግሞ ከፉንባው ዳርቻወች ላይ የሚውሉ ዐጽቅ ንዑስ ረቲድ (minor axis) ይባላል።  የንዑስ ረቲድ ግማሽ ደግሞ ንፍቀንዑስ ረቲድ ወይም ንፍቀኑስ ረቲድ (semi-minor axis) ይባላል። 
4. የዐብይ ረቲድ ጫፎች የፉንባው ፊጣወች (vertices) ሲባሉ፣ የንዑስ ረቲድ ጫፎች ደግሞ የፉንባው አበርፊጣወች (co-vertices) ይባላሉ። 

የፉንባ ብያኔ

በክብ (circle) ብያኔ (definition)መሠረት ክብ (circle) ማለት መሃል (center) ከሚባል አንድ ነጥብ ያላቸው ርቀት እኩል የሆነ የወልሰቴ ነጥቦች ኢዶ (locus of coplanar points) ነው።   በሌላ አባባል ክብ ማለት መሃል ከሚባል አንድ ነጥብ ያላቸው ርቀት ወልፌክ (constant) የሆነ የወልሰቴ ነጥቦች ኢዶ ነው።  ወልፌክ (constant) ማለት ቋሚ፣ የማይለወጥ ማለት ሲሆን፣ ቃሉ የተገኘው ወልፌከኛ (ማለትም ያው፣ አንድ አይነት) ከሚለው የኦሮምኛ ቃል ነው።

በተመሳሳይ መንገድ በፉንባ (ellipse) ብያኔ (definition) መሠረት ፉንባ (ellipse) ማለት አቲኮች (foci) ከሚባሉ ሁለት ነጥቦች ያሏቸው ርቀቶች ድምር ወልፌክ (constant) የሆነና ከአቲኮች ርርቀት የበለጠ (larger than distance between) የወልሰቴ ነጥቦች ኢዶ (locus of coplanar points) ነው።

የፉንባ ሙለት

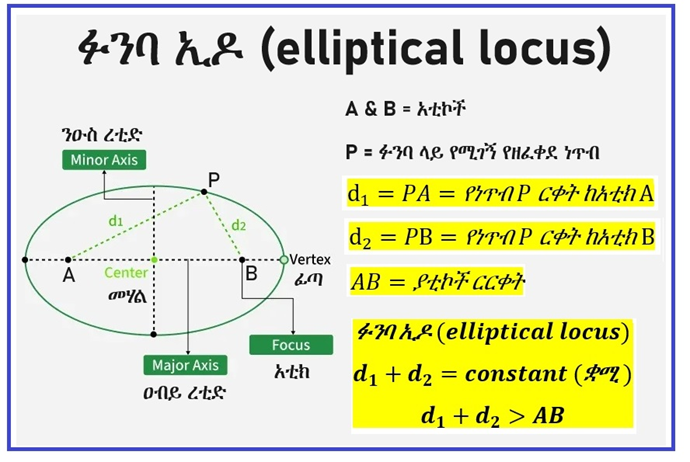
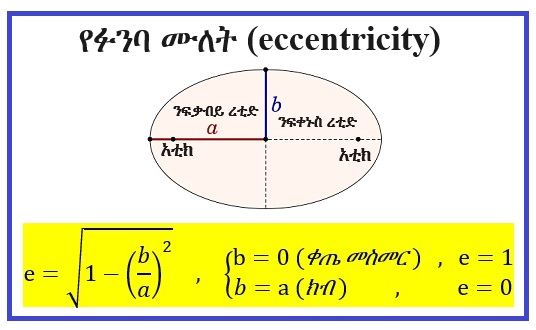
የፉንባ ሙለት (eccentricity) ማለት የፉንባውን ሞላላነት፣ ማለትም ፉንባው ከክብነት ያለውን ርቀት የሚገልጽ እሴት ሲሆን፣ በፊደል e ይወከላል።  የፉንባ ሙለት (eccentricity) እሴት የፉፓው አቲኮች ርርቀት(distance between foci) እና የፉፓው ዐብይ ረቲድ(major axis) ነጸቅ (ratio) ነው፣ ማለትም የፉፓው አቲኮች ርርቀት በፉፓው ዐብይ ረቲድ ሲካፈል (divided) የሚገኘው እሴት (value) ነው። ነጸቅ ወይም ንጽቀት (ratio) የሚለው ቃል የተገኘው ንጽጽራዊትልቀትከሚለው ሲሆን፣ ግሱም ሲረባ ነጸቀ፣ ንጽቅ፣ ነጻቂ፣ ንጸቃ፣ /ንጽቀት/ እያለ ይሄዳል። 

ያንድ ፉንባ ንፍቃብይ ረቲድ (semi-major axis) a ከሆነና የፉንባው ንፍቀኑስ ረቲድ (semi-minor axis) ደግሞ b ከሆነ፣  የፉንባው ሙለት (eccentricity) በሚከተለው ቀመር (formula) ይሰጣል። 

ከፉንባ ሙለት (eccentricity) ቀመር (formula) መረዳት እንደሚቻለው የፉንባ ሙለት ማግዘም እሴት (maximum value) e = 1 ሲሆን፣ ሚንሰም እሴቱ (minimum value) ደግሞ e = 0 ነው።   

1. የፉንባ ሙለት ማግዘም (maximum) የሚሆነው (ማለትም e = 1 የሚሆነው)፣ የፉፓው ንፍቀኑስ ረቲድ (b = 0) ሲሆን ነው።  በሌላ አባባል የፉንባ ሙለት e = 1 የሚሆነው፣ ፉንባው ቀጤ መስመር (straight line) ሲሆን ነው።  አሁንም በሌላ አባባል ቀጤ መስመር (straight line) ማለት ሙለቱ e = 1 የሆነ ልዩ ፉንባ (special ellipse) ነው ማለት ነው።   
2.  የፉንባ ሙለት ሚንሰም (maximum) የሚሆነው (ማለትም e = 0 የሚሆነው)፣ የፉፓው ንፍቀኑስ ረቲድ (b = 1) ሲሆን ነው።  በሌላ አባባል የፉንባ ሙለት e = 0 የሚሆነው፣ ፉንባው ክብ (circle) ሲሆን ነው።  አሁንም በሌላ አባባል ክብ (circle) ማለት ሙለቱ e = 0 የሆነ ልዩ ፉንባ (special ellipse) ነው ማለት ነው።  
3. የፉንባ ሙለት ከዳዶ (0) በመነሳት ቶኮ (1) እስከሚሆን ድረስ እየጨመረ ሲሄድ፣ ፉንባው የበለጠና የበለጠ እየሞለለ ይሄዳል።   

የፉንባ ስፋት

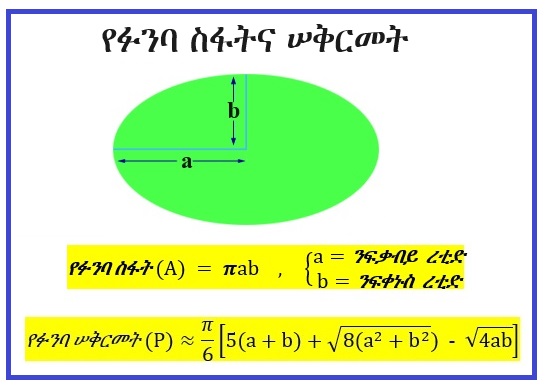
ያንድ ፉንባ ንፍቃብይ ረቲድ (semi-major axis) a ከሆነና የፉንባው ንፍቀኑስ ረቲድ (semi-minor axis) ደግሞ b ከሆነ፣  የፉንባው ስፋት (eccentricity) በሚከተለው ቀመር (formula) ይሰጣል። 

የፉንባ ሠቅርመት የቅርበዛ ቀመሮች

አቃረበ የሚለውን ለማርባት ይመች ዘንድ ቅርበዛ (approximation) እንለዋለን። ግሱም ሲረባ ቀረበዘ (approximate)፣ ቅርብዝ (ቅርቡዝ) [approximated]፣ ቀርባዚ (ቀርባዥ) [approximator]፣ ቅርበዛ (approximating) እያለ ይሄዳል።

የፉንባ ሠቅርመት (circumference) ማለት ፉንባው ዙርያውን ያለው ርዝመት ማለት ነው።  የፉንባ ሠቅርመት ሌላኛው ስሙ የፉንባ ዙርዝመት (perimeter) ነው። 

የፉንባን ሠቅርመት እቅጩን (precisely) የሚሰጥ ቀመር (formula) የለም።  በሌላ በኩል ግን የፉፓን ሠቅርመት በተለያዩ የቅርበዛ ቀመሮች (approximate formulas) በቅርበዛ (approximately) ማግኘት ይቻላል። 

ያንድ ፉንባ ንፍቃብይ ረቲድ(semi-major axis) a ከሆነና የፉንባው ንፍቀኑስ ረቲድ(semi-minor axis) ደግሞ b ከሆነ፣  የፉንባው ሠቅርመት (circumference) በሚከተሉት የቅርበዛ ቀመሮች (approximation formulas) /ይሰጣል/። 

1. ቀመር (1) የሚያገለግለው a እና b ተቀራራቢ ሲሆኑ፣ ማለትም ፉንባው ከሞላ ጎደል ክብ ሲሆን ነው። 
2. ቀመር (2) የሚሰጠው እሴት ከፉንባው እቅጭ ሠቅርመት የበለጥ ሲሆን፣ ቀመር (3) የሚሰጠው እሴት ደግሞ ያነሰ ነው።  ስለዚህም a እና b ተቀራራቢ በማይሆኑበት ጊዜ፣ ማለትም የፉንባው ሙለት ከፍተኛ በሚሆንበት ጊዜ፣ ቀመር (2) እና ቀመርን (3) ተጠቅሞ አማካያቸውን (average) በመውሰድ የተሻለ ቅርበዛ (approximation) ማግኘት ይቻላል።  
3. ከሁሉም የተሻለው ቅርበዛ (approximation) ደግሞ የሦስቱንም ቀመሮች አማካይ (average) መውሰድ ሲሆን፣ ይህን ሐሳብ ያቀረብኩት ደግሞ እኔ ራሴ መስፍን አረጋ ነኝ።    

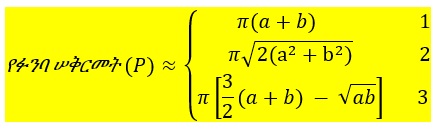
በሌላ በኩል ደግሞ ታዋቂው ህንዳዊ ሒሳብሲነኛ (mathematician) ስሪኒቫሳ ራማኑጃን (Srinivasa Ramanujan) የፉንባን ሠቅርመት በከፍተኛ ቅርበዛ (very high approximation) የሚሰጡ ሁለት ቀመሮች (formulas) ቀምሯል።  እነዚህም ቀሮች አንደኛውና ሁለተኛው የራማኑጃን ቀመሮች (Ramanujan formulas) ይባላሉ። 

ማጠቃለያ

መስፍን አረጋ
mesfinamharic.com
mesfin.arega@gmail.com